Matching LRF Scans by Shape

Shapes from two consecutive scans are matched against each other to track shapes. The state-of-the-art shape matching employed is combined by a structural, qualitative representation of all polylines. This creates a larger context than matching objects on an individual basis and, hence, prevents mixups in the presence of multiple similar objects.

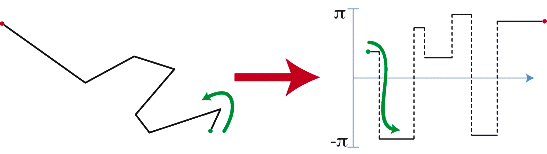
Shape matching constitutes out of two processes: First, polylines are transformed into a tangent-space representation and compared to each other to ontain a measure of similarity. Second, a correspondence of polylines is computed respected the cyclic order of objects in the scan.

Similarity of Polylines

Similarity of polylines is computed in tangent-space. A tangent-space representation is a multi-valued step function representing a polyline independent of position.

A similarity measure for two polylines can be deduced from a correspondence of arcs. Therefore, the two polylines' arcs are matched against each other. The desired overall matching is said to constitute out of 1-to-1, 1-to-many, and many-to-1 corresondences of arcs. This allows to apply the technique of Dynamic Programming to compute the best correspondence of arcs. The computation makes use of a basic similarity measure of two arcs, which is is given as a difference function in tangent space.

Example:

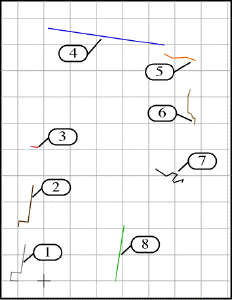Polylines in scan #1	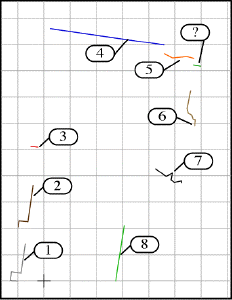Polylines in scan #2

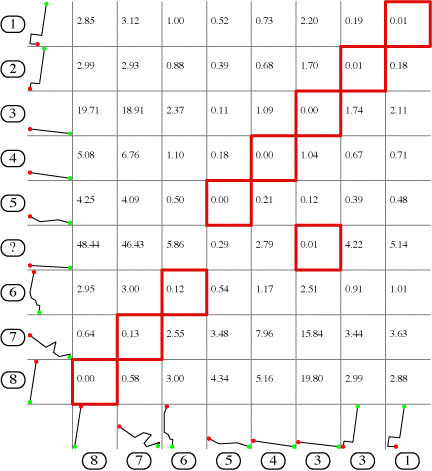
Table of individual similarities, highest similarities highlighted (Higher numbers denote higher dissimilarity).

Matching Respecting Cyclic Ordering

To determine a matching of all polylines involved, it is respected that any admissible matching must not violate the cyclic order of polylines as they a acquired from the LRF. So, we seek to compute the correspondence of polylines P[1],...P[n] and P'[1],...P'[m] minimizing the overall sum of similarities P[i] and P'[j]. This can again be achieved by applying Dynamic Programming.

Coming back to the example presented above, the best correspondence of the polyline marked ? and the one marked 3, would inhibit any matching of polylines 5 against 5, 4 against 4, ..., and 1 against 1. In the process of determining an admissible matching of polylines, the—tentative—correspondence between polyline ? and 3 is weighted against the correspondences it inhibits. So, it can be concluded here that is best to not match polyline ? at all, which is the correct decision.